C++ 使用 Parallel For 多线程计算圆周率 - Monte Carlo

计算圆周率是个老掉牙的课题. 最为简单的直接易懂的无非就是通过 Monte Carlo 来随机撒点然后计算在圆内的点和总共的点数的比例再乘于4就能得到一个估计的值. 当然随机数的产生一定要质量好虽然计算机没有真正的随机算法但是一些伪随机算法比如 xorshift 就很不错.

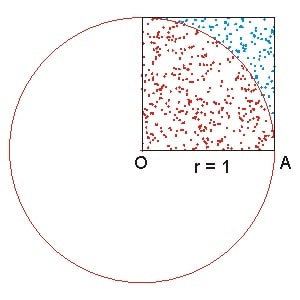
Monte-Carlo01

单机版本的计算简单明了.

int monte_carlo_count_pi(int n)
{
	int c = 0;
	for (int i = 0; i < n; i ++)
	{
		double x = (double)rand() / (RAND_MAX);
		double y = (double)rand() / (RAND_MAX);
		if (x * x + y * y <= 1.0)
		{
			c++;
		}
	}
	return c;
}

然后借助于 Parallel.For 我们就可以很简单的把这个算法并行化了.

int main()
{
	srand(time(NULL));// 种子
	const int N1 = 1000;
	const int N2 = 100000;
	int n = 0;
	int c = 0;
	Concurrency::critical_section cs;
	// N1 值小于 N2 会有比较好的多线程效率
	Concurrency::parallel_for(0, N1, [&](int i)
	{
		int t = monte_carlo_count_pi(N2);
		cs.lock(); // race condition
		n += N2;   // total sampling points
		c += t;    // points fall in the circle
		cs.unlock();
	});
	cout < < "圆周率 约等于 " << setprecision(9) << (double)c / n * 4.0 << endl;
	return 0;
}

完整代码在 github: https://github.com/DoctorLai/coding_exercise/blob/master/parallel_monte_carlo_pi.cpp

实现的关键就在于把所要撒的点分成每一份 N2 个点数然后我们需要有一个critical_section 来保证同时只有一个线程来修改我们统计的两个变量.

如果你运行这个程序你就会发现CPU利用率 90% 左右如果只是单线程的话计算 N1*N2=100000K 则需要很久. 这样简单的使用Parallel.For 则可以大大的利用多核CPU. 比如这个HPZ800.

能得到多少倍提升呢? 我们还需要考虑阿姆达尔定律

英文: C++ 使用 Parallel For 多线程计算圆周率 - Monte Carlo

本文一共 313 个汉字, 你数一下对不对.

C++ 使用 Parallel For 多线程计算圆周率 – Monte Carlo. (AMP 移动加速版本)
上一篇: 在PHP里执行SQL文件
下一篇: CLOUDFLARE 又有免费的保护可用 - DNSSEC

赞赏我的几个理由.

¥ 打赏支持

扫描二维码，分享本文到微信朋友圈