Teaching Kids Programming – Tower of Hanoi via Recursion (Math Induction Proof of Minimal Number of Moves)

Teaching Kids Programming: Videos on Data Structures and Algorithms

Introduction to Hanoi Tower Problem

Hanoi Tower is a famous math puzzle. There are three rods and N disks. The smaller size of disks need to be always ontop of bigger ones. And one move you are only allowed to move one disk.

The question is: what is the minimal number of moves to move all disks from first rod (A) to last rod (C), and what are the moves (what is the strategy).

Recursive Algorithm to Solve Hanoi Towers

The algorithm to solve the Hanoi Towers is pretty simple: Let’s use T(N) to represent the number of minimal moves required to move N disks from rod A to rod C.

1. First we need to move the Top N-1 Disks from Rod A to B which takes T(N-1).
2. And then we move the bottom disk N to C directly (this takes one move).
3. And last, we move the Top N-1 disks in step 1 from Rod B to Rod C. This takes another T(N-1)

Thus we have this Recursive formula:

and 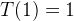obviously.

Math Induction Proof of Hanoi Tower Fomula

Math Induction is a power tool to prove a math equation. Let’s look at the first few values of T given the above Recursion relations: T(N)=2*T(N-1)+1.

T(1)=1
T(2)=3
T(3)=7
T(4)=15
T(5)=31

We can guess

Apparently, T(1)=1 stands. And let’s assume N=k stands, and we have this for N=k+1

and
and
and
thus, we have prove the case when N=k+1.

Recursive Algorithm to Simulate the Hanoi Tower Moves

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def hanoiTowersMove(n, src, dest, temp):
    if n == 1:
        print("Move disk {} from {} to {}".format(1, src, dest))
        return
    hanoiTowersMove(n - 1, src, temp, dest)
    print("Move disk {} from {} to {}".format(n, src, dest))
    hanoiTowersMove(n - 1, temp, dest, src)
 
"""
Move disc 1 from  A to  C
Move disc 2 from  A to  B
Move disc 1 from  C to  B
Move disc 3 from  A to  C
Move disc 1 from  B to  A
Move disc 2 from  B to  C
Move disc 1 from  A to  C
"""

def hanoiTowersMove(n, src, dest, temp):
    if n == 1:
        print("Move disk {} from {} to {}".format(1, src, dest))
        return
    hanoiTowersMove(n - 1, src, temp, dest)
    print("Move disk {} from {} to {}".format(n, src, dest))
    hanoiTowersMove(n - 1, temp, dest, src)

"""
Move disc 1 from  A to  C
Move disc 2 from  A to  B
Move disc 1 from  C to  B
Move disc 3 from  A to  C
Move disc 1 from  B to  A
Move disc 2 from  B to  C
Move disc 1 from  A to  C
"""

The time complexity is as this is the minimal number of moves for N disks in Hanoi Towers.

–EOF (The Ultimate Computing & Technology Blog) —