Teaching Kids Programming – The Birthday Candles Problem (Three Algorithms)

Teaching Kids Programming: Videos on Data Structures and Algorithms

The Birthday Candles Problem

If a person blows 1 candle at Age 1, 2 candles at Age 2, 3 candles at Age 3, then what is the year of the birthday if he/she has blown total 231 candles.

This can be solved using three algorithms/approaches.

The Bruteforce Algorithm

We can try brute forcing (perform a linear search) the year and compute the sum, until it reaches T (total) or exceed it.

def f(T):
    year = 0
    total = 0
    while total < T:
        year += 1
        total += year
    return year if total == T else -1

To understand the number of iterations, notice that the total is essentially the sum of the first n natural numbers, where n is the number of years. This sum is known to be . The loop stops when this sum is greater than or equal to T. So, we’re looking for the smallest n such that:

Solving this quadratic inequality gives us the smallest n that satisfies the condition. Since this is essentially forming a series, the number of iterations is proportional to the square root of T because you’re solving for n in a quadratic equation. This means the time complexity of the loop is O(√T).

The Binary Search Algorithm

We can binary search the range [1, T].

def f(T):
    L = 1
    R = T
    while L <= R:
        M = L + R >> 1
        s = (M + 1) * M >> 1
        if s == T:
            return M
        if s < T:
            L = M + 1
        else:
            R = M - 1
    return -1

The key to understanding the time complexity lies in the while loop and how quickly the range between L and R is reduced.

• Each iteration of the while loop approximately halves the search range.
• The initial range of values is from 1 to T.
• The number of times you can halve T until you get down to 1 (the smallest possible range) is

So, the while loop, which dominates the time complexity, runs in O(log T) time. Thus, the overall time complexity of the function is O(log T).

The Quadratic Equation Solver

Given the Year n, and the total T, we have a quadratic equation for the first n accumulated sum:

We know there are two roots: and
When we have real roots. And since the root is positive, we only consider the .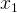

We compute the value of 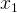and check if it is a whole integer. This can be done via pythons’ is_integer method. The time/complexity is O(1) considering that the square root is amortized O(1) constant.

def f(T):
    a = 1
    b = 1
    c = -2 * T
    x = (-b + (b*b-4*a*c)**0.5)/(2*a)
    if x.is_integer():
        return int(x)
    return -1

See the variation of this problem: Teaching Kids Programming – Another Birthday Candles Problem

–EOF (The Ultimate Computing & Technology Blog) —