Teaching Kids Programming – Sum of First N Even Numbers (with Mathematic Induction)

Teaching Kids Programming: Videos on Data Structures and Algorithms

Yesterday we talked about summing up the first N odd numbers, we know that the equation is N*N. Today, let’s talk about the sum of the first N Even numbers instead.

The total sum of the First 2*N numbers is (1+2N)*2N/2 = N+2N^2. Then we deduct N*N (First N Odd Numbers), we have the sum of the first N Even Numbers which is N^2+N.

We can prove this using the Arithmetic progression formula to compute the sum of 2 + 4 + 6 + … 2N:

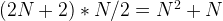
Sum of First N Even Numbers using Mathematic Induction

Proposition: .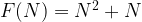
Base case: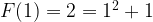
Let’s assume stands,

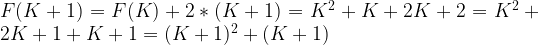
Therefore, we can conclude that the formula to compute the first N even numbers is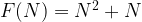

Python O(1) Algorithm to Compute the Sum of First N Even Numbers

O(1) time and O(1) space as both time and space complexity do not change regarding to input size.

1
2

def sumOfFirstEvenNumbers(N):
  return N*N+N

def sumOfFirstEvenNumbers(N):
  return N*N+N

Python O(N) Algorithm to Sum the First N Even Numbers

We can sum the even values by using an accumulator:

1
2
3
4
5

def sumOfEvenNumbers(N):
  ans = 0
  for i in range(2, 2*N+1, 2):
    ans += i
  return ans

def sumOfEvenNumbers(N):
  ans = 0
  for i in range(2, 2*N+1, 2):
    ans += i
  return ans

This is a linear algorithm, if the input size is large, this algorithm will run for a while to finish.

We can use math.pow(a, b) or a**b (works only for integers) in Python to compute the value of (a to the power of b).

–EOF (The Ultimate Computing & Technology Blog) —