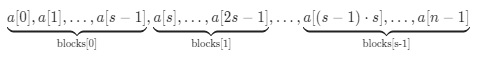Teaching Kids Programming: Videos on Data Structures and Algorithms
Given an integer array nums, handle multiple queries of the following types:
Update the value of an element in nums.
Calculate the sum of the elements of nums between indices left and right inclusive where left <= right.
Implement the NumArray class:
Example 1:
Input
[“NumArray”, “sumRange”, “update”, “sumRange”]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
Output
[null, 9, null, 8]Explanation
Naive Solution: Mutable List Range Query – O(1) Update – O(N) Sum Range
The most intuitive way is to store the numbers as it is – and perform the sum range using bruteforce algorithm. This takes O(N) time to compute the range sum – but O(1) to update.
1 2 3 4 5 6 7 8 9 | class NumArray: def __init__(self, nums: List[int]): self.nums = nums def sumRange(self, i, j): return sum(self.nums[i:j+1]) def update(self, idx, val): self.nums[idx] = val |
class NumArray:
def __init__(self, nums: List[int]):
self.nums = nums
def sumRange(self, i, j):
return sum(self.nums[i:j+1])
def update(self, idx, val):
self.nums[idx] = valO(1) update and O(N) sum range.
Mutable List Range Query with Prefix Sum: O(N) Update – O(1) Sum Range
We can use prefix sum to obtain O(1) constant time for sumRange operation – however, to update a number requires O(N) time to update the prefix sum:
1 2 3 4 5 6 7 8 9 10 11 12 | class NumArray: def __init__(self, nums: List[int]): self.nums = nums self.prefix = [0] + list(accumulate(self.nums)) def sumRange(self, i, j): return self.prefix[j + 1] - self.prefix[i] def update(self, idx, val): for i in range(idx + 1, len(self.prefix)): self.prefix[i] += val - self.nums[idx] self.nums[idx] = val |
class NumArray:
def __init__(self, nums: List[int]):
self.nums = nums
self.prefix = [0] + list(accumulate(self.nums))
def sumRange(self, i, j):
return self.prefix[j + 1] - self.prefix[i]
def update(self, idx, val):
for i in range(idx + 1, len(self.prefix)):
self.prefix[i] += val - self.nums[idx]
self.nums[idx] = valO(N) update and O(1) sum range. The prefix sum is initialized using the accumulate function. We prepend a zero to avoid the prefix[to-1] having the negative index.
Mutable List Range Query with Sqrt Decomposition: O(1) Update –
We can allocate
To update an element, we can just update the number and update the sum for that block. To compute the range sum – we at most need to add
To sum up the range – we can add the block sum (and skip
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | class NumArray: def __init__(self, nums: List[int]): self.nums = nums self.n = math.ceil(sqrt(len(nums))) self.blocks = [0] * (len(nums) // self.n + 1) for i in range(len(nums)): self.blocks[i//self.n] += nums[i] def update(self, idx: int, val: int) -> None: self.blocks[idx // self.n] += val - self.nums[idx] self.nums[idx] = val def sumRange(self, left: int, right: int) -> int: ans = 0 x = left while x <= right: if x % self.n == 0 and x + self.n <= right: ans += self.blocks[x // self.n] x += self.n # skip to next block else: ans += self.nums[x] x += 1 return ans |
class NumArray:
def __init__(self, nums: List[int]):
self.nums = nums
self.n = math.ceil(sqrt(len(nums)))
self.blocks = [0] * (len(nums) // self.n + 1)
for i in range(len(nums)):
self.blocks[i//self.n] += nums[i]
def update(self, idx: int, val: int) -> None:
self.blocks[idx // self.n] += val - self.nums[idx]
self.nums[idx] = val
def sumRange(self, left: int, right: int) -> int:
ans = 0
x = left
while x <= right:
if x % self.n == 0 and x + self.n <= right:
ans += self.blocks[x // self.n]
x += self.n # skip to next block
else:
ans += self.nums[x]
x += 1
return ansO(1) update and
This problem can also be solved by Segment Tree or Fenwick Tree – which has
+--------------------+------------------------+----------------------+ | Name | Update Time Complexity | Query Time Compexity | +====================+========================+======================+ | Naive 1 | O(1) | O(n) | +--------------------+------------------------+----------------------+ | Naive 2 | O(n) | O(1) | +--------------------+------------------------+----------------------+ | Segment Tree | log(n) | log(n) | +--------------------+------------------------+----------------------+ | Fenwick Tree | log(n) | log(n) | +--------------------+------------------------+----------------------+ | Sqrt Decomposition | O(1) | sqrt(n) | +--------------------+------------------------+----------------------+
–EOF (The Ultimate Computing & Technology Blog) —
Last Post: Teaching Kids Programming - High Accuracy Multiplication Algorithm (Multiply Strings)
Next Post: Teaching Kids Programming - Converting (Binary) Trees to Undirectional Graphs via DFS and BFS Algorithms