Teaching Kids Programming – Silver Ratio and Pell Numbers (Metal Quadratic Equation)

Teaching Kids Programming: Videos on Data Structures and Algorithms

We know the Golden Ratio 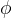is defined as the fraction 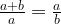where 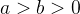if we set 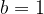then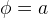

Quadratic function 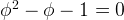, we know there are two roots to quadratic equation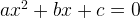

Root 1: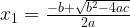
Root 2: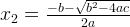

We take the positive root which is 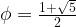which is approximately 1.618

We also learned previously that the golden ratio exists in the Fibonacci numbers:

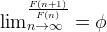
Metal Quadratic Equation

Let’s define the quadratic equation 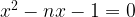the metal ratio equation:

when 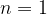we have the Golden Ratio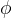
when 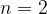we have the Silver Ratio which is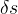
when 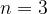we have the Bronze Ratio.
and so on…

The (positive) root for the metal quadratic equation is:

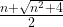, which can be rewritten as the continued fraction:

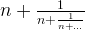
Pell Number and Silver Ratio

Let’s take the Silver Ratio Equation: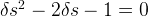

We can solve the positive root is 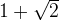which is approximately 2.414

The Pell Numbers are quite similar to Fibonacci numbers except each number in the Pell Number sequence is equal to two times its previous number plus the one before:

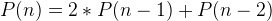
where the first two Pell numbers are:

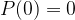
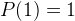
The first few Pell Numbers are: 0, 1, 2, 5, 12, 29, 70, 169, … (if the first two numbers are both 2, then we have Pell-Lucas Numbers)

If we keep going on..

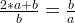which is the silver ratio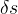
aka.

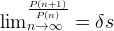
So, we can use this method to estimate the value of the silver ratio 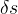also the value of the square root of two .

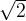Compute Pell Number in Recursion

We can implement the Pell Number (similar to Fibonacci Number) in Recursion and then can be improved with memoziation which makes it Dynamic Programming Algorithm (Top Down).

@cache
def pell(n):
    if n == 0:
        return 0
    if n == 1:
        return 1
    return 2*pell(n - 1) + pell(n - 2)

Most modern compilers will probably optimise this into the iterative manner:

def pell(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, 2 * b + a
    return a

–EOF (The Ultimate Computing & Technology Blog) —