Teaching Kids Programming: Videos on Data Structures and Algorithms
Given a MinMax implementation, one problem is that there are two situations that we need to handle separately: maximizing and minimizing. We can implement both scenarios in a same recursive function, or two separate function where max calls the min and min calls the max.
The NegaMax is a simplified implementation of the MinMax, based on the following observation:
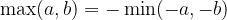
Thus, we can set to always find maximum value in the NegaMax algorithm but we have to negate the sign when passing to next round.
1 2 3 4 5 6 7 | def negamax(self, state, depth, player): if depth == 0 or self.isEnd(state): return evalState(state) score = -math.inf for act in self.actions(state): score = max(score, self.negamax(self.succ(state, act), depth - 1, -player) return score |
def negamax(self, state, depth, player):
if depth == 0 or self.isEnd(state):
return evalState(state)
score = -math.inf
for act in self.actions(state):
score = max(score, self.negamax(self.succ(state, act), depth - 1, -player)
return scoreThe negamax simplifies the implementation of minmax by combining two scenarios. Both players can be treated as finding the maximal value of the nodes – as we negate the value into next recursive call. The above is the Negamax Base Algorithm which can be used to implement the Alpha Beta Pruning.
Game Theory – Game Algorithms
- Teaching Kids Programming – Alpha Beta Pruning Algorithm on NegaMax (Game Theory)
- Teaching Kids Programming – NegaMax Algorithm (Game Theory)
- Teaching Kids Programming – Alpha-Beta Pruning Algorithm (Game Theory)
- Teaching Kids Programming – Define Tic Tac Toe using Game Theory Terminologies
- Teaching Kids Programming – Introduction to Two Players Zero-Sum Game (Number Halving)
- Teaching Kids Programming – MinMax Algorithm in Game Tree (Game Theory, Tic Tac Toe)
–EOF (The Ultimate Computing & Technology Blog) —
loading...
Last Post: Teaching Kids Programming - Alpha-Beta Pruning Algorithm (Game Theory)
Next Post: Teaching Kids Programming - Alpha Beta Pruning Algorithm on NegaMax (Game Theory)