Teaching Kids Programming: Videos on Data Structures and Algorithms
What is a Minimum Spanning Tree?
A Graph (G) is a collection of vertex V and edges E that is . We want to build a tree T with all vertex where T is a subset of G i.e.
A tree does not have a cycles, and therefore, with N vertex, we need N-1 edges. The total weights by picking up N-1 edges are:
Kruskal’s Minimum Spanning Tree Algorithm
With Kruska, we can pick N-1 edges to build the Minimum Spanning Tree (MST):
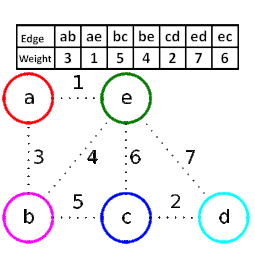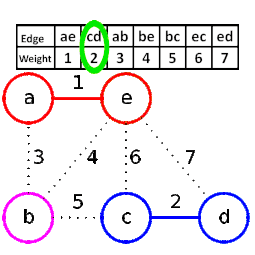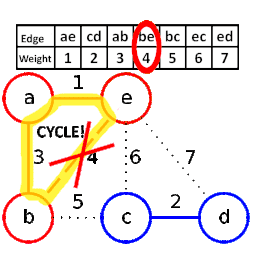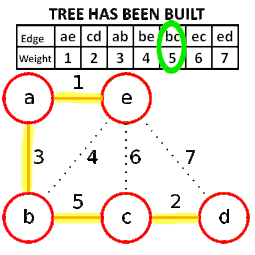
The steps of applying the Kruskal’s MST Algorithm:
- First, we sort the edges in the ascending order of weights.
- Build a forest F with all vertex only (no edges yet – each vertex is a separate tree)
- While F is not connected:
- – Then, we start picking the smallest edge from the S and that does not form a cycle in the F
- – Add it to F and remove it from S.
- Last, when we have N-1 edges, we have the minimum spanning tree (MST).
The animation process for Kruskal MST algorithm:
The Psuedo code for Kruskal MST algorithm:
1 2 3 4 5 6 7 8 9 10 11 | def kruskal(V, E): F = ∅ for e in E: F.add({e}) # sort by weight in ascending order E.sort(lambda key: key.weight) for u, v in E: if findParent(u) != findParent(v): F:= F ∪ {(u, v)} ∪ {(v, u)} merge(findParent(u), findParent(v)) return F |
def kruskal(V, E):
F = ∅
for e in E:
F.add({e})
# sort by weight in ascending order
E.sort(lambda key: key.weight)
for u, v in E:
if findParent(u) != findParent(v):
F:= F ∪ {(u, v)} ∪ {(v, u)}
merge(findParent(u), findParent(v))
return FThe time complexity for Kruskal MST algorithm is as we need to sort the E edges. To check if a edge causes a cycle, we can use the Disjoint Set – and by the compression of path, the time complexity to find parent, and merge two groups is trivial.
As there could be at most edges, and thus Thus the time complexity for Kruskal MST algorithm can also be represented by .
The space complexity is V as we need to use Disjoint Set.
Correctness Proof for the Kruskal’s MST Algorithm
We are choosing the smallest edge E to connect two components – let’s say this is not part of the MST, and the correct edge is E’. So E’ will form a cycle and then we can replace E’ with E as it is the smallest. Thus, E should be part of the MST – and Tree T we obtain by picking the edges form a minimum spanning tree.
We can also build a MST by Prim’s algorithm: Teaching Kids Programming – Introduction to Prim’s Minimum Spanning Tree (Graph Algorithm)
–EOF (The Ultimate Computing & Technology Blog) —
loading...
Last Post: Teaching Kids Programming - Silver Ratio and Pell Numbers (Metal Quadratic Equation)
Next Post: Teaching Kids Programming - Introduction to Prim's Minimum Spanning Tree (Graph Algorithm)
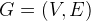 . We want to build a tree T with all vertex
. We want to build a tree T with all vertex 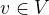 where T is a subset of G i.e.
where T is a subset of G i.e. 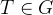
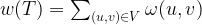
 in the ascending order of weights.
in the ascending order of weights.
 as we need to sort the E edges. To check if a edge causes a cycle, we can use the
as we need to sort the E edges. To check if a edge causes a cycle, we can use the 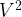 edges, and thus
edges, and thus 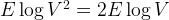 Thus the time complexity for Kruskal MST algorithm can also be represented by
Thus the time complexity for Kruskal MST algorithm can also be represented by 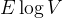 .
.