Teaching Kids Programming: Videos on Data Structures and Algorithms
Koko loves to eat bananas. There are n piles of bananas, the ith pile has piles[i] bananas. The guards have gone and will come back in h hours.
Koko can decide her bananas-per-hour eating speed of k. Each hour, she chooses some pile of bananas and eats k bananas from that pile. If the pile has less than k bananas, she eats all of them instead and will not eat any more bananas during this hour.
Koko likes to eat slowly but still wants to finish eating all the bananas before the guards return.
Return the minimum integer k such that she can eat all the bananas within h hours.
Example 1:
Input: piles = [3,6,7,11], h = 8
Output: 4Example 2:
Input: piles = [30,11,23,4,20], h = 5
Output: 30Example 3:
Input: piles = [30,11,23,4,20], h = 6
Output: 23Constraints:
1 <= piles.length <= 10^4
piles.length <= h <= 10^9
1 <= piles[i] <= 10^9You are given a list of integers piles and an integer k. piles[i] represents the number of bananas on pile i. On each hour, you can choose any pile and eat r number of bananas in that pile. If you pick a pile with fewer than r bananas, it still takes an hour to eat the pile.
Return the minimum r required such that you can eat all the bananas in less than or equal to k hours.
Constraints
n ≤ 100,000 where n is the length of piles
n ≤ k
Example 1
Input
piles = [6, 4, 3]
k = 5
Output
3
Explanation
At r = 3 bananas per hour, we can eat the first pile in 2 hours, eat the second in 2 hours, and eat the last pile in 1 hour.Try making a function which could return true if for a given value of ‘r’ it is possible to eat all the bananas within ‘k’ hours.
Binary Search?
What is the possible range of r?
You can check all r in this range and still be quite fast.
Binary Search Algorithm to Eat Banans/Apples in K Hours
Given that we eat r in one hour (speed), we can compute the total time using the following function which has time complexity 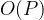 .
.
1 2 | def f(r): return sum(ceil(i / r) for i in piles) |
def f(r):
return sum(ceil(i / r) for i in piles)Then, we can bruteforce the speed r from 1 to the max(P). Overall time complexity is 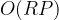 .
.
1 2 3 4 5 6 | L = 1 R = max(piles) for i in range(L, R + 1): if f(i) <= k: return i |
L = 1
R = max(piles)
for i in range(L, R + 1):
if f(i) <= k:
return iWe can also binary search the R so overall time complexity is 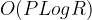 . If we can finish all the fruits in K hours when we eat R in one hour, certainly we can finish the fruit when R is bigger. So the search space is monotonous. When
. If we can finish all the fruits in K hours when we eat R in one hour, certainly we can finish the fruit when R is bigger. So the search space is monotonous. When 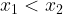 so
so 
1 2 3 4 5 6 7 | while L < R: M = (L + R) // 2 if f(M) <= k: R = M else: L = M + 1 return L |
while L < R:
M = (L + R) // 2
if f(M) <= k:
R = M
else:
L = M + 1
return L–EOF (The Ultimate Computing & Technology Blog) —
loading...
Last Post: Teaching Kids Programming - Count Nodes Equal to Average of Subtree via Recursive Depth First Search Algorithm
Next Post: Teaching Kids Programming - Maximum Sum of K Numbers from Front and Back of Array (Sliding Window Algorithm)