Quick Sort is a comparison sorting method, on average, the complexity is . In worst cases, e.g. when the array of elements are already sorted, it is degraded into comparisons, although this is rare. Because Quick sort can be implemented in in-place partitioning algorithm, and it can benefit from local cache due to sequential and localized references, Quick sort is generally practically fast then other approaches.
Quick sort is an efficient sorting algorithm, however not stable, because it will swap the order of two idential elements. Quick sort can be implemented in recursive and iterative approach. However, the recursive approach is generally fast and easy to implement, which is often the preferred approach. It uses additional space.
The idea of Quick sort is simple: first find an reference element in the array, we call it the pivot. The easiest way is to pick the first one, but sometimes, if it is already sorted, picking the first element will degrade the Quick sort into . Therefore, the middle element of the array is often chosen. The index of the mid element can be computed as (l + r) >> 1, however this will gives integer overflow if the left-most and right-most index is big. To solve this, by incurring slightly an extra arithmetic operations, l + (r – l) >> 1.
Given the pivot element, we in place divide the array into two halves, with the left list all elements no bigger than the pivot element, and the right list all elements no smaller than the pivot element. The next thing would be to recursively sort the left and right list.
By dividing the array into two, we use an in place partitioning algorithm. We have to cursors initialized to its leftmost and rightmost index sort. We increment the left cursor if the current element at the left cursor is smaller than the pivot element, similarly, we decrement the rightmost cursor if the current element at the right cursor is bigger than the pivot element.
If the left cursor is still smaller than the right cursor, it means we have two elements which are not in the right place. We can simply swap them to make the left list contains all elements no bigger than the pivot and the right list contains all elements no smaller than the pivot.
Iteratively until the left cursor is bigger than the right cursor, we have these two sub lists. The next thing would be recursively sort the sub-lists if they are not empty.
The Python code below illustrates very clearly the Quick sort.
#!/usr/bin/env python
"""
https://helloacm.com
QuickSort.py
Quick Sorting Algorithm
01/Dec/2012
"""
from random import *
from time import *
seed()
x = []
for i in range(0, 100):
x.append(randint(0, 100))
def qsort(x, l, r):
i = l
j = r
p = x[l + (r - l) / 2] # pivot element in the middle
while i <= j:
while x[i] < p: i += 1
while x[j] > p: j -= 1
if i <= j: # swap
x[i], x[j] = x[j], x[i]
i += 1
j -= 1
if l < j: # sort left list
qsort(x, l, j)
if i < r: # sort right list
qsort(x, i, r)
return x
start = time()
print "Before: ", x
x = qsort(x, 0, len(x) - 1)
print "After: ", x
print "%.2f seconds" % (time() - start)
Similar to this [post], we time the efficiency of the Quick sort, it is efficient enough to beat other simple sorts (such as selection, bubble). We sort the 100 elements, and it only uses 0.04 seconds, which is faster than Bogo sort, obviously.
Before: [92, 18, 2, 67, 0, 77, 22, 70, 99, 92, 56, 66, 10, 81, 81, 49, 46, 76, 96, 97, 39, 15, 31, 65, 48, 22, 97, 20, 89, 29, 91, 2, 16, 34, 20, 24, 85, 85, 23, 86, 11, 21, 74, 17, 97, 70, 57, 44, 36, 18, 26, 29, 1, 39, 6, 66, 15, 68, 10, 60, 42, 92, 99, 11, 91, 22, 84, 52, 99, 46, 36, 21, 22, 41, 19, 33, 13, 39, 69, 95, 80, 78, 64, 78, 15, 78, 92, 7, 10, 75, 56, 67, 34, 44, 29, 57, 1, 8, 84, 18] After: [0, 1, 1, 2, 2, 6, 7, 8, 10, 10, 10, 11, 11, 13, 15, 15, 15, 16, 17, 18, 18, 18, 19, 20, 20, 21, 21, 22, 22, 22, 22, 23, 24, 26, 29, 29, 29, 31, 33, 34, 34, 36, 36, 39, 39, 39, 41, 42, 44, 44, 46, 46, 48, 49, 52, 56, 56, 57, 57, 60, 64, 65, 66, 66, 67, 67, 68, 69, 70, 70, 74, 75, 76, 77, 78, 78, 78, 80, 81, 81, 84, 84, 85, 85, 86, 89, 91, 91, 92, 92, 92, 92, 95, 96, 97, 97, 97, 99, 99, 99] 0.04 seconds
Here is an alternative Python implementation of QuickSort Algorithm, using Recursion, in a Pythonic manner – which is easier to remember, and easier to write on whiteboard if you are asked on any coding interviews.
How to implement the Quicksort in C++? How to Find out the Most Frequent Subtree Sum using Depth First Search Algorithm?
And, how about Javascript Quicksort? Javascript Coding Exercise: The QuickSort Implementation in Javascript
–EOF (The Ultimate Computing & Technology Blog) —
loading...
Last Post: Codeforces: B. Internet Address
Next Post: Codeforces: A. System Administrator
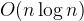 . In worst cases, e.g. when the array of elements are already sorted, it is degraded into
. In worst cases, e.g. when the array of elements are already sorted, it is degraded into 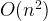 comparisons, although this is rare. Because Quick sort can be implemented in in-place partitioning algorithm, and it can benefit from local cache due to sequential and localized references, Quick sort is generally practically fast then other
comparisons, although this is rare. Because Quick sort can be implemented in in-place partitioning algorithm, and it can benefit from local cache due to sequential and localized references, Quick sort is generally practically fast then other 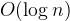 space.
space.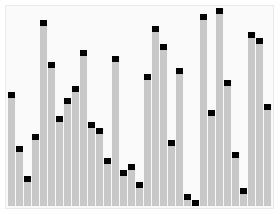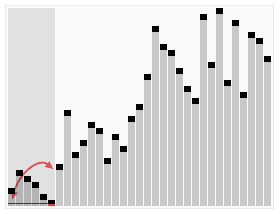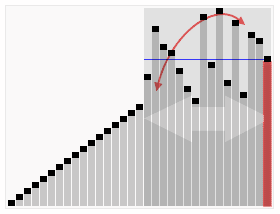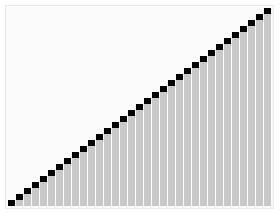
Hi,
If you set pivot = min(x) then the code will run indefinitely.
It is random, so it is certain that not every iteration chooses min(x) as the pivot.
hi
my english is bad but thanks for this code its more important for me 😀
thanks
not a problem. glad that it is useful to you.