You are asked to find the number of order pairs (x, y) such that,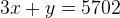 
and x, y are natural numbers which also satisfy 
.
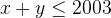Mathematics
This shouldn’t be too complex. If we let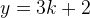 
where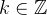 
.
If we mod 3, we then have this:
.
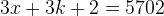
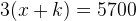
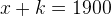So, all the solutions are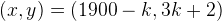 
where where .
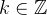Since 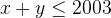so we have 
,
.
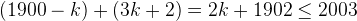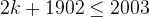
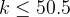We have 51 solutions because k can be from 0 to 50 inclusive.
Bruteforce
If you don’t like maths, then write a small piece of C++ code that verifies this via bruteforce all possibilities within the conditions:
int sum = 0;
for (int x = 1; x <= 2002; x ++) {
for (int y = 1; y <= 2003 - x; y ++) {
if (3 * x + y == 5702) sum ++;
}
}
cout << sum << endl;
–EOF (The Ultimate Computing & Technology Blog) —
645 wordsLast Post: How to Remove all elements of val From a Linked List?
Next Post: ScriptUnit - VBScript/JScript Unit Tests Runner