There is a 2D binary matrix M filled with 0’s and 1’s, your task is to find the largest square containing all 1’s and return its area. For example,
1 1 1 1
1 1 0 0
0 0 1 1
1 1 0 1
should return 4.
Dynamic Programming
You could easily come up with a bruteforce approach that iterates all possible sub-squares in the entire area. This could take ages if the given matrix is large. If we use function f(i, j) to denote the maximum length of the square if the square has the right-bottom corner at (i, j), then we have the following DP formula:
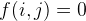
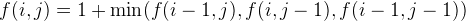
Once we have the maximum length size, we get its area. We can use STL:vector to store 2D elements easily like this:
1 | vector< vector<int> > f(h + 1, vector<int>(w + 1, 0)); |
vector< vector<int> > f(h + 1, vector<int>(w + 1, 0));
The size of the Matrix is m, n, however we can extend the DP matrix by 1 in both dimensions so it is easier without boundary checking.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | class Solution { public: int maximalSquare(vector<vector<char>>& matrix) { int h = matrix.size(); if (h == 0) return 0; int w = matrix[0].size(); if (w == 0) return 0; int m = 0; vector< vector<int> > f(h + 1, vector<int>(w + 1, 0)); for (int i = 1; i <= h; i ++) { for (int j = 1; j <= w; j ++) { if (matrix[i - 1][j - 1] == '0') { f[i][j] = 0; } else { f[i][j] = 1 + min(f[i][j - 1], min(f[i - 1][j - 1], f[i - 1][j])); m = max(m, f[i][j]); // store the maximum length } } } return m * m; } }; |
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int h = matrix.size();
if (h == 0) return 0;
int w = matrix[0].size();
if (w == 0) return 0;
int m = 0;
vector< vector<int> > f(h + 1, vector<int>(w + 1, 0));
for (int i = 1; i <= h; i ++) {
for (int j = 1; j <= w; j ++) {
if (matrix[i - 1][j - 1] == '0') {
f[i][j] = 0;
} else {
f[i][j] = 1 + min(f[i][j - 1], min(f[i - 1][j - 1], f[i - 1][j]));
m = max(m, f[i][j]); // store the maximum length
}
}
}
return m * m;
}
};For example, given input
1 1 0 1 1 1 1 1 1
First step, is to extend the DP matrix by 1.
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
And, according to the DP formula, we have the following outcomes:
0 0 0 0 0 1 1 0 0 1 2 0 0 1 2 2
The min function makes sure only squares are cascaded further. The overall complexity is O(n2) and so is the space complexity.
–EOF (The Ultimate Computing & Technology Blog) —
Last Post: How to List Process Owners using VBScript + WMI Object?
Next Post: Milestone - The 1000 Posts