Teaching Kids Programming – Estimate the Golden Ratio via Fibonacci Numbers in Python

Teaching Kids Programming: Videos on Data Structures and Algorithms

The Golden Ratio, in mathematics, is often denoted using the symbol 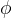. The approximate value of the Golden Ratio is often known as 1.618, which can be obtained by solving the following equation.

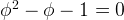which gives two roots.

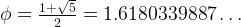or

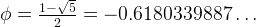
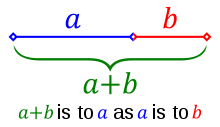
Two line segments (lengths are a and b, respectively) are said to be in golden ratio if the lengths satisfy the following.

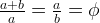
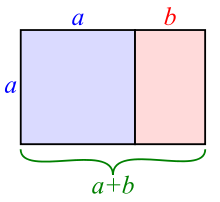
Similarly, the golden rectangle should meet the following:

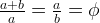
We all know that the Fibonacci numbers are defined as:

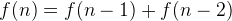
for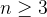

and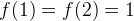

The ratio between the number in the series and its successor tends to converge to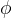

For example, any three continuous numbers in the series can be defined as b, a, b + a.

Therefore, we find that, the ratio between the first two and the last two numbers are

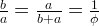
Let’s verify this in a small Python code via computing the first 20 numbers of the Fibonacci Sequences.

#!/usr/bin/env python

a = 1
b = 1
N = 20

for i in range(N):
    a, b = b, a + b
    print(b * 1.0 / a)

Let’s observe the output and we can see the Estimation of the Golden Ratio converges pretty fast.

2.0
1.5
1.66666666667
1.6
1.625
1.61538461538
1.61904761905
1.61764705882
1.61818181818
1.61797752809
1.61805555556
1.61802575107
1.61803713528
1.61803278689
1.61803444782
1.6180338134
1.61803405573
1.61803396317
1.61803399852
1.61803398502

References:

http://en.wikipedia.org/wiki/Golden_ratio

–EOF (The Ultimate Computing & Technology Blog) —