We all know that the total number of solution to pick combination of n items out of m items is C(m, n), and sometimes denoted as or .
We can easily write an iterative function to compute the value. The following C function comb requires a two-dimensional array to store the intermediate results. Please noted that the value of C(m, 0) = 1, meaning that picking zero items out of any is always one solution. Also,
C(m, 0) = 1 C(m, m) = 1 C(0, m) = 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | #define MAX 100 int comb(int m, int n) { int mat[MAX][MAX]; int i, j; if (n > m) return 0; if( (n == 0) || (m == n) ) return 1; for( j = 0; j < n; j ++) { mat[0][j] = 1; if (j == 0) { for (i = 1; i<= m - n; i ++ ) mat[i][j] = i + 1; } else { for (i = 1; i<= m - n; i ++) mat[i][j] = mat[i - 1][j] + mat[i][j - 1]; } } return (mat[m - n][n - 1]); } |
#define MAX 100
int comb(int m, int n) {
int mat[MAX][MAX];
int i, j;
if (n > m) return 0;
if( (n == 0) || (m == n) ) return 1;
for( j = 0; j < n; j ++) {
mat[0][j] = 1;
if (j == 0) {
for (i = 1; i<= m - n; i ++ ) mat[i][j] = i + 1;
}
else {
for (i = 1; i<= m - n; i ++) mat[i][j] = mat[i - 1][j] + mat[i][j - 1];
}
}
return (mat[m - n][n - 1]);
}Of course, this can be rewritten in recursive form but I wouldn’t recommend this because of the performance.
You could add the following to shorten the outer loop count but I doubt any performance gains doing this since there is an overhead recursion calls.
1 | if (n + n > m) return comb(m, m - n); |
if (n + n > m) return comb(m, m - n);
This is based on the formula: C(m, n) = C(m, m – n).
The combinations can also be solved by Pascal Triangle, and therefore, the following recurrence formula is useful.
1 | C(m, n) = C(m - 1, n) + C(m - 1, n - 1); |
C(m, n) = C(m - 1, n) + C(m - 1, n - 1);
To just show you the idea, the following is the inefficient recursion C function to compute the combinations based on the pascal triangle.
1 2 3 4 5 6 | int pascal(int m, int n) { int i, j; if (n > m) return 0; if( (n == 0) || (m == n) ) return 1; return pascal(m - 1, n) + pascal(m - 1, n - 1); } |
int pascal(int m, int n) {
int i, j;
if (n > m) return 0;
if( (n == 0) || (m == n) ) return 1;
return pascal(m - 1, n) + pascal(m - 1, n - 1);
}This can be converted into iterative approach, which is far more efficient.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | int pascal(int m, int n) { int ans[MAX][MAX]; int i, j; if (n > m) return 0; if( (n == 0) || (m == n) ) return 1; for (i = 0; i <= n; i ++) { ans[0][i] = 1; ans[i][0] = 1; } for (i = 1; i <= m; i ++) { for (j = 1; j <= n; j ++) { ans[i][j] = ans[i - 1][j] + ans[i - 1][j - 1]; } } return ans[m][n]; } |
int pascal(int m, int n) {
int ans[MAX][MAX];
int i, j;
if (n > m) return 0;
if( (n == 0) || (m == n) ) return 1;
for (i = 0; i <= n; i ++)
{
ans[0][i] = 1;
ans[i][0] = 1;
}
for (i = 1; i <= m; i ++)
{
for (j = 1; j <= n; j ++)
{
ans[i][j] = ans[i - 1][j] + ans[i - 1][j - 1];
}
}
return ans[m][n];
}As you probably notice, the i-th row only depends the result of (i-1)-th row, therefore, we don’t need to keep two dimensional array for intermediate results.
1 2 3 4 5 6 7 8 9 10 11 12 13 | int pascal(int m, int n) { int ans[MAX]; int i, j; if (n > m) return 0; if( (n == 0) || (m == n) ) return 1; ans[0] = 1; for (i = 1; i <= m; i ++) { for (j = 1; j <= n; j ++) { ans[j] = ans[j] + ans[j - 1]; } } return ans[n]; } |
int pascal(int m, int n) {
int ans[MAX];
int i, j;
if (n > m) return 0;
if( (n == 0) || (m == n) ) return 1;
ans[0] = 1;
for (i = 1; i <= m; i ++) {
for (j = 1; j <= n; j ++) {
ans[j] = ans[j] + ans[j - 1];
}
}
return ans[n];
}This approach is concise and only requires one dimensional array. However, the complexity is still O(mn). Such optimisation technique can also be found in Dynamic Programming when the solution to the current problem only depends on its previous sub-solution.
–EOF (The Ultimate Computing & Technology Blog) —
loading...
Last Post: Test Javascript On/Off in PHP via POST
Next Post: How to Use VBScript to Delete Duplicate Excel Rows with Another Less Column Value
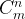 or
or 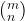 .
.
I’m afraid it is a bug:
_ ans[] is not initialized, introducing potential bugs due to random values
_ the loop
for (j = 1; j <= n; j ++)
{
ans[j] = ans[j] + ans[j – 1];
}
screws ans[] content
proof: like this: ans[j] is always greater than ans[j-1], inacceptable for a line of Pascal's triangle
ultimate proof: test my version against yours and see by yourself…
The code for int pascal(int m, int n) is full of bugs !
Here’s a correct version:
int pascal(int m, int n)
{
int ans[MAX];
int i, j;
if (n > m) return 0;
if (n + n > m)
{
n = m – n; // pascal(m, n) == pascal(m, m-n) – choose min(n, m-n)
}
if (n == 0) return 1; // n == m case now impossible
ans[0] = 1;
for (i = 1; i <= n; i++)
{
ans[i] = 0; //ans[] array MUST be initialized !
}
for (i = 1; i <= m; i++)
{
for (j = n; 0 < j; –j) // j loop must be done backwards !
{
ans[j] += ans[j – 1];
}
}
return ans[n];
}
It is not a bug. Just a recursion to illustrate the idea. Recursion can be optimised by iteration.
I keep claiming it’s full of bugs !
1) ans[] MUST be initialized, or random values will poison the algorithm
2) the iteration on j
for (j = 1; j <= n; j ++)
{
ans[j] = ans[j] + ans[j – 1];
}
screws ans[] content – loop MUST be done backwards !
Just check my version against yours and see by yourself !
Please ignore my previous post (a -j should be a –j)
The code for int pascal(int m, int n) is full of bugs !
Here’s a correct version:
int pascal(int m, int n)
{
int ans[MAX];
int i, j;
if (n > m) return 0;
if (n + n > m)
{
n = m – n; // pascal(m, n) == pascal(m, m-n) – choose min(n, m-n)
}
if (n == 0) return 1; // n == m case now impossible
ans[0] = 1;
for (i = 1; i <= n; i++)
{
ans[i] = 0; //ans[] array MUST be initialized !
}
for (i = 1; i <= m; i++)
{
for (j = n; 0 < j; –j) // j loop must be done backwards !
{
ans[j] += ans[j – 1];
}
}
return ans[n];
}