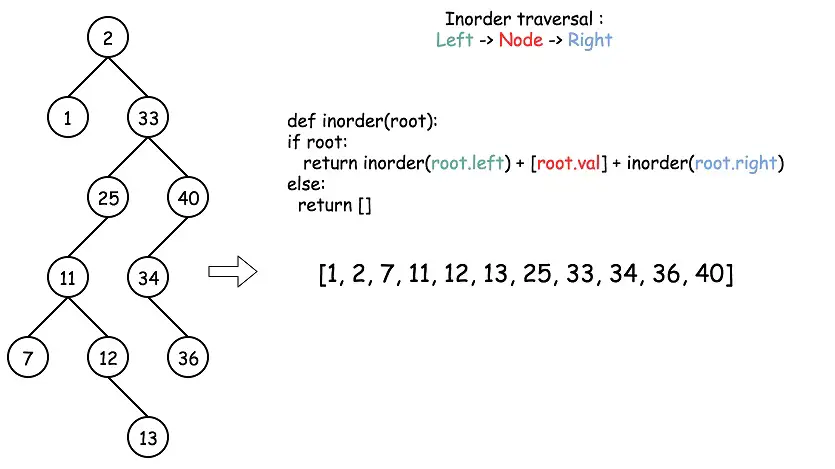
A Binary Search Tree (BST) is a commonly used data structure that can be used to search an item in O(LogN) time. A BST should have the following characteristics: its left nodes are smaller than the root and its right nodes are larger than the root.
If we perform an inorder traversal: left nodes first, current node, and then right nodes – we will have a fully sorted sequence.
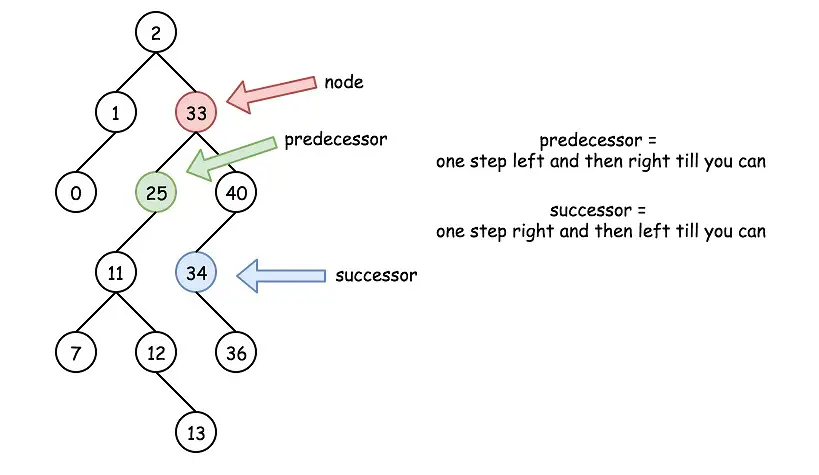
To find the Predecessor or Sucessor Node of a BST – we can perform the following algorithms:
Find the Predecessor Node of a Binary Search Tree
The predecessor node is the largest node that is smaller than the root (current node) – thus it is on the left branch of the Binary Search Tree, and the rightmost leaf (largest on the left branch).
The C++ function to find the predecessor node of a BST node:
1 2 3 4 5 6 | TreeNode* predecessor(TreeNode* root) { if (!root) return nullptr; root = root->left; while (root->right) root = root->right; return root; } |
TreeNode* predecessor(TreeNode* root) {
if (!root) return nullptr;
root = root->left;
while (root->right) root = root->right;
return root;
}And below is the Java implementation to get the predecessor node of a Binary Search Tree:
1 2 3 4 5 6 | public int predecessor(TreeNode root) { if (root == null) return null; root = root.left; while (root.right != null) root = root.right; return root; } |
public int predecessor(TreeNode root) {
if (root == null) return null;
root = root.left;
while (root.right != null) root = root.right;
return root;
} Python function to get the predecessor of a BST:
1 2 3 4 5 6 7 | def predecessor(root): if root is None: return None root = root.left while root.right: root = root.right return root |
def predecessor(root):
if root is None:
return None
root = root.left
while root.right:
root = root.right
return rootFind the Successor Node of a Binary Search Tree
On the other hand, the successor node is the smallest node that is bigger than the root/current – thus it is on the right branch of the BST, and also on the leftmost leaf (smallest on the right branch).
The C++ function to get the successor node of a Binary Search Tree.
1 2 3 4 5 6 | TreeNode* successor(TreeNode* root) { if (!root) return nullptr; root = root->right; while (root->left) root = root->left; return root; } |
TreeNode* successor(TreeNode* root) {
if (!root) return nullptr;
root = root->right;
while (root->left) root = root->left;
return root;
}Java method to get the successor:
1 2 3 4 5 6 | public int successor(TreeNode root) { if (root == null) return null; root = root.right; while (root.left != null) root = root.left; return root; } |
public int successor(TreeNode root) {
if (root == null) return null;
root = root.right;
while (root.left != null) root = root.left;
return root;
} Finally, the below is the Python implementation of getting a sucessor node of a BST:
1 2 3 4 5 6 7 | def successor(root): if root is None: return None root = root.right while root.left: root = root.left return root |
def successor(root):
if root is None:
return None
root = root.right
while root.left:
root = root.left
return rootAll implementation of finding successor or predecessor takes O(1) constant space and run O(N) time (when BST is just a degraded linked list) – however, on average, the complexity is O(LogN) where the binary tree is balanced.
Finding successor or predecessor is very useful – for example, we can use this to delete a node in a binary search tree.
See also: Compute the Inorder Successor of a Binary Tree
–EOF (The Ultimate Computing & Technology Blog) —
Last Post: Algorithms to Detect Pattern of Length M Repeated K or More Times in a String
Next Post: Using the Windows Hardware Tool to Error Checking and Optimize Your HardDrives