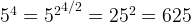Source: http://oj.leetcode.com/problems/powx-n/
Implement Pow(x, n) which computes The given parameter x is a 64-bit double and n is a 32-bit integer.
The quick solution may be so obvious, using bruteforce, iterate n times that multiplies x and gives a straightforward result.
1 2 3 4 5 6 7 8 9 | class Solution { public: double pow(double x, int n) { // brute force - TOO SLOW double r = 1; for (int i = 0; i < n; i ++) r *= x; return r; } }; |
class Solution {
public:
double pow(double x, int n) {
// brute force - TOO SLOW
double r = 1;
for (int i = 0; i < n; i ++) r *= x;
return r;
}
};However, this yields TIME LIMIT EXCEEDED on inputs like because the exponential is very large.
How to improve this? One optimisation hint is base on the fact that:
if n is even. For example,
How about n is odd, we can just multiply one time the base x.
So, each iteration, we square the base x and reduces the exponential n to its half, which will give an algorithm complexity of log(2^n).
We can also use binary logic and operation x & 1 == 1 to check if x is odd rather than x % 2 == 1 which I think is a bit slower than the first one.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | class Solution { public: double pow(double x, int n) { // check the sign of n bool plus = n >= 0; n = plus ? n : -n; double r = 1; while (n > 0) { // if odd if (n & 1 == 1) { r *= x; } // reduce the exponential to its half n /= 2; // square the base x *= x; } // if n < 0, should return 1.0/x^n return plus ? r : 1.0 / r; } }; |
class Solution {
public:
double pow(double x, int n) {
// check the sign of n
bool plus = n >= 0;
n = plus ? n : -n;
double r = 1;
while (n > 0) {
// if odd
if (n & 1 == 1) {
r *= x;
}
// reduce the exponential to its half
n /= 2;
// square the base
x *= x;
}
// if n < 0, should return 1.0/x^n
return plus ? r : 1.0 / r;
}
};–EOF (The Ultimate Computing & Technology Blog) —
loading...
Last Post: Minimum Depth of Binary Tree by using Recursive Depth First Search and Iterative Breadth First Search Algorithms
Next Post: Coding Exercise - N Queen Problem - C++ - Bit Logics - Shortest and Fastest Solution - Online Judge
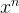 The given parameter x is a 64-bit double and n is a 32-bit integer.
The given parameter x is a 64-bit double and n is a 32-bit integer.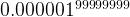 because the exponential is very large.
because the exponential is very large.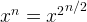 if n is even. For example,
if n is even. For example,