Question: Implement integer square root for int sqrt(int x)
There are many ways to compute the integer square root. But if you don’t bother, you can always cheat the compilers (online judge), but don’t do this in your interviews!
The cheat ways:
Well, most programming languages have sqrt for float numbers (single or double precision), we can simply write:
1 2 3 4 5 6 7 8 9 | #include <math.h> class Solution { public: int sqrt(int x) { // add std:: namespace to distinguish from current sqrt() return (int)std::sqrt(x); } }; |
#include <math.h>
class Solution {
public:
int sqrt(int x) {
// add std:: namespace to distinguish from current sqrt()
return (int)std::sqrt(x);
}
};In Java,
1 2 3 4 5 | public class Solution { public int sqrt(int x) { return (int)Math.sqrt(x); } } |
public class Solution {
public int sqrt(int x) {
return (int)Math.sqrt(x);
}
}Or ( )
1 2 3 4 5 6 7 | #include <math.h> class Solution { public: int sqrt(int x) { return (int)pow(x, 0.5); } }; |
#include <math.h>
class Solution {
public:
int sqrt(int x) {
return (int)pow(x, 0.5);
}
};Exhaustive Search:
One may come up with a brute-force search quickly. We just have to try numbers from 1 until the square of this number is larger than the output.
1 2 3 4 5 6 7 8 9 10 11 | #include <math.h> typedef unsigned long long ULONG; class Solution { public: int sqrt(int x) { ULONG a = 1; while (a * a <= x) a ++; return --a; } } |
#include <math.h>
typedef unsigned long long ULONG;
class Solution {
public:
int sqrt(int x) {
ULONG a = 1;
while (a * a <= x) a ++;
return --a;
}
}Please note that we have defined a unsigned long long type to hold the intermediate result of a * a so that the result won’t overflow (too big for a 32-bit integer).
Well, the above seems unlikely to accept in online judge. But surprisingly, this is an accepted solution. Why is that? The int type is 32-bit signed integer, which gives the maximum value 2^31 – 1 = 2147483647. The square root of this is just 46340.9, which means that at most 46341 iterations, we have the correct integer root. This is trivial in modern processors, which can be done in million seconds.
The improvement:
We notice that a * a is expensive, how to get rid of that?
Therefore, we can just add 2 to a variable delta and add it to current variable a to get the square of a + 1.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #include <math.h> typedef unsigned long long ULONG; class Solution { public: int sqrt(int x) { ULONG a = 1; ULONG delta = 3; while (a <= x) { a += delta; // (a + 1)^2 delta += 2; } return delta / 2 - 1; } } |
#include <math.h>
typedef unsigned long long ULONG;
class Solution {
public:
int sqrt(int x) {
ULONG a = 1;
ULONG delta = 3;
while (a <= x) {
a += delta; // (a + 1)^2
delta += 2;
}
return delta / 2 - 1;
}
}The above improvements remove the multiplication and use additions only, which is often implemented in some PC boards where time is not a critical issue.
Binary Search:
The above algorithm complexity is and it is still very slow when given integer is large. The binary search can shorten this to .
Binary search is one of the most important algorithms, and in order for it to work, it requires continuous search space (e.g. numbers sorted)
In the domain of integer square roots, we can find that easily:
is less than for any given non-negative integers.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <math.h> typedef unsigned long long ULONG; class Solution { public: int sqrt(int x) { ULONG l = 0, r = x; while (l <= r) { ULONG mid = l + (r - l) / 2; // (l + r) / 2; ULONG midmid = mid * mid; // check if x falls into [mid^2, (mid + 1)^2) if ((midmid <= x) && (x < (mid + 1) * (mid + 1))) return mid; if (midmid > x) { r = mid - 1; } else { l = mid + 1; } } } } |
#include <math.h>
typedef unsigned long long ULONG;
class Solution {
public:
int sqrt(int x) {
ULONG l = 0, r = x;
while (l <= r) {
ULONG mid = l + (r - l) / 2; // (l + r) / 2;
ULONG midmid = mid * mid;
// check if x falls into [mid^2, (mid + 1)^2)
if ((midmid <= x) && (x < (mid + 1) * (mid + 1))) return mid;
if (midmid > x) {
r = mid - 1;
} else {
l = mid + 1;
}
}
}
}With binary search, every iteration will narrow the search space to its half. The mid = (l + r) / 2 may overflow so we can use mid = l + (r – l) / 2 to accomplish the same thing.
Newton’s method:
Binary search is a great improvement, but it still is too slow finding the solution. Modern processors have hardware square roots algorithm implemented and most of them are based on Newtons’ equation:
As we can see, with every iteration of Newton’s equation, we find a closer root of
We have if we want to find the square root of a.
The derivative
and we have initial guess .
For example,
The Newton’s method converges rapidly and is considered very efficient.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | #include <math.h> typedef unsigned long long ULONG; class Solution { public: int sqrt_newton(int x) { if (x==0) return x; double dividend = x; double val = x; double last; do { last = val; val = (val + dividend / val) * 0.5; } while(abs(val - last) > 1e-9); // precision return (int)val; } } |
#include <math.h>
typedef unsigned long long ULONG;
class Solution {
public:
int sqrt_newton(int x) {
if (x==0) return x;
double dividend = x;
double val = x;
double last;
do {
last = val;
val = (val + dividend / val) * 0.5;
} while(abs(val - last) > 1e-9); // precision
return (int)val;
}
}We check the current iteration with the last , if the difference is smaller than e.g. 1e-9 (EPSILON), then we think we have got the desired precision.
Another similar problem is to check if a given integer is a valid perfect square.
Reference:
http://en.wikipedia.org/wiki/Newton’s_method
–EOF (The Ultimate Computing & Technology Blog) —
loading...
Last Post: C Sharp Extension Method
Next Post: Understanding Tail Recursion - Visual Studio C++ - Assembly View
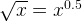 )
)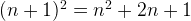
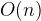 and it is still very slow when given integer is large. The binary search can shorten this to
and it is still very slow when given integer is large. The binary search can shorten this to 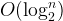 .
.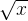 is less than
is less than 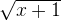 for any given non-negative integers.
for any given non-negative integers.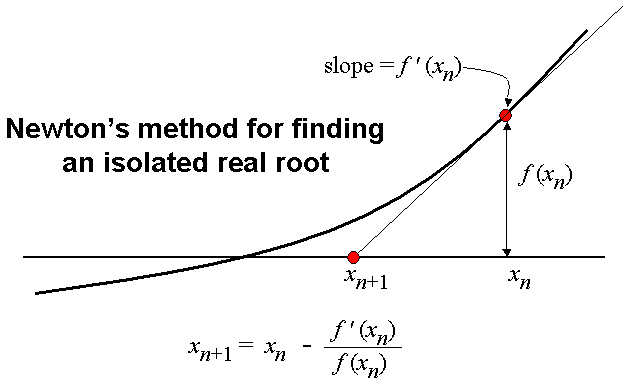
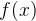
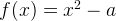 if we want to find the square root of a.
if we want to find the square root of a.
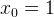 .
.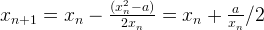

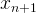 with the last
with the last 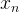 , if the difference is smaller than e.g. 1e-9 (EPSILON), then we think we have got the desired precision.
, if the difference is smaller than e.g. 1e-9 (EPSILON), then we think we have got the desired precision.