C++ Implementation of Trie Data Structure using Hash Map

trie-example

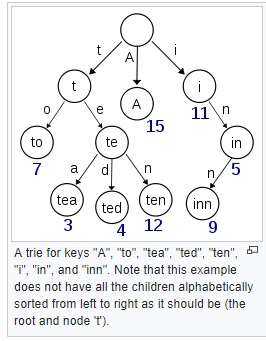
Trie is a useful data structure allow us to search a given word or check if any words start with prefix in O(N) efficient time. The following is the C++ implementation of Trie Class which is based on unordered_map hash map instead of a fix-size e.g. 26 children. The advantages of doing so is that we can use the Trie class in basically any character set (not just English lowercase/uppercase).

class Trie {
    public:
    Trie() {
        leaf = false;
    }

    unordered_map<char, Trie*> children;
    bool leaf;
    
    void add(string s) {
        auto root = this;
        for (const auto &n: s) {
            if (!root->children[n]) {
                root->children[n] = new Trie();
            }
            root = root->children[n];
        }
        root->leaf = true;
    }

    bool exists(string word) {
        auto root = this;
        for (const auto &n: word) {
            if (!root->children[n]) {
                return false;
            }
            root = root->children[n];
        }        
        return root && root->leaf;
    }

    bool startswith(string p) {
        auto root = this;
        for (const auto &n: p) {
            if (!root->children[n]) {
                return false;
            }
            root = root->children[n];
        }        
        return root != NULL;      
    }
};

The space complexity for Trie class is often O(MN) where M is the number of strings to add and the N is the average length of the words. The time complexity of Trie is O(N) where N is the length of the given string to lookup, add or check if any starts with it (prefix check).

We can use the Trie in the following way:

Trie trie;
trie.add("hello");
trie.startswith("hel"); // true
trie.exists("hel"); // false

Trie Algorithms Implementations:

• Teaching Kids Programming – Python Implementation of Trie Data Structure (Prefix Tree)
• C++ Implementation of Trie Data Structure using Hash Map
• The Beginners’ Guide to Trie: How to Use the Trie in C++?
• Trie Class Data Structure in Python
• GoLang: Implement Trie (Prefix Tree)

–EOF (The Ultimate Computing & Technology Blog) —