Algorithm to Compute the Pascal Triangle’s values

ACMer

10 years ago

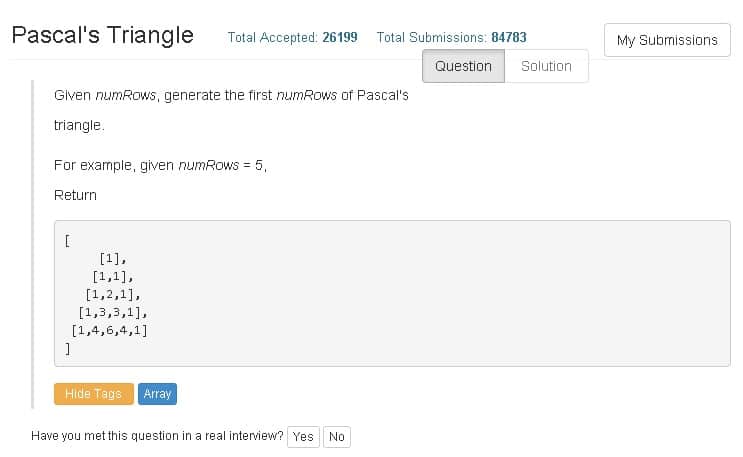
The puzzle is to generate the first few numRows rows of Pascal’s Triangle.

C++ Coding Exercise – Interview – Pascal’s Triangle

Do you need to keep each row in separate variables (row vector)? Apparently no. The trick here is to have a row vector that represents the last row (n) and base on that construct a new row (n + 1). After each iteration, the row vector is pushed back to the result vector. Of course, for each new row, we increase the size of the vector by one element (number 1 is pushed to the right).

class Solution {
public:
    vector<vector<int> > generate(int numRows) {
        vector<vector<int> > r;
        if (numRows <= 0) {
            return r;
        }
        vector<int> cur;
        cur.push_back(1);
        r.push_back(cur);
        for (int i = 0; i < numRows - 1; i ++) {
            for (int j = cur.size() - 1; j > 0; j --) {
                cur[j] += cur[j - 1];
            }             
            cur.push_back(1); // right-most 1
            r.push_back(cur);
        }
        return r;
    }
};

class Solution {
public:
    vector<vector<int> > generate(int numRows) {
        vector<vector<int> > r;
        if (numRows <= 0) {
            return r;
        }
        vector<int> cur;
        cur.push_back(1);
        r.push_back(cur);
        for (int i = 0; i < numRows - 1; i ++) {
            for (int j = cur.size() - 1; j > 0; j --) {
                cur[j] += cur[j - 1];
            }             
            cur.push_back(1); // right-most 1
            r.push_back(cur);
        }
        return r;
    }
};

Example: 1 – 3 – 3 – 1 ==> 1 – (1+3) – (3+3) – (3+1) and we add 1 to the right at the end of each iteration.

To return the N-th row, we can use a simplified solution: Compute the Nth Row of a Pascal’s Triangle using Dynamic Programming Algorithm

Pascal Triangle Implementations:

–EOF (The Ultimate Computing & Technology Blog) —

446 words
Last Post: Introduction to programming - C Exercise - Circuit
Next Post: Code Snippet Auto Complete on Switch Statement using enum in Visual Studio

The Permanent URL is: Algorithm to Compute the Pascal Triangle’s values (AMP Version)