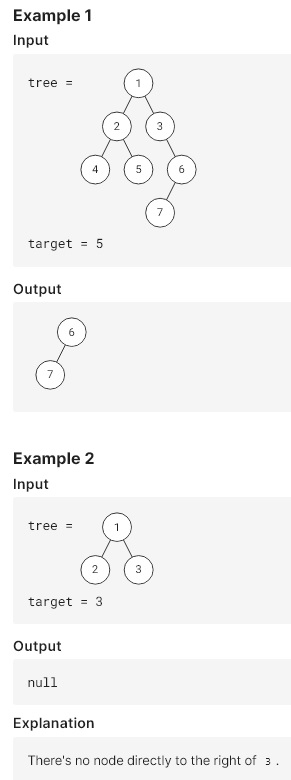
You are given a binary tree root containing unique values, and an integer target. Find the node with value target and return the node that’s directly right of it on its level. If the target node doesn’t exist or if it’s already in the rightmost position, return null.
Constraints
0 ≤ n ≤ 100,000 where n is the number of nodes in root
Finding the Node on the Right using Breadth First Search Algorithm
Like other (Binary) Tree problems, we can use Breadth First Search Algorithm to solve the problem perfectly. A BFS performs the search level-by-level, so we can expand all the nodes in the current queue (they are belonging to same leve). If current node is the target, we either return the next dequed node or None if it hasn’t got one.
C++ Code to implement the BFS Algorithm to Find a Next Node on the right in a Binary Tree. The time and space complexity are both O(N) where N is the number of the nodes in the binary tree.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | /** * class Tree { * public: * int val; * Tree *left; * Tree *right; * }; */ Tree* findRightNode(Tree* tree, int target) { if (!tree) return NULL; queue<Tree*> Q; Q.push(tree); while (!Q.empty()) { auto sz = Q.size(); for (int i = 0; i < sz; ++ i) { auto p = Q.front(); Q.pop(); if (p->val == target) { return i == sz - 1 ? NULL : Q.front(); } if (p->left) Q.push(p->left); if (p->right) Q.push(p->right); } } return NULL; } |
/**
* class Tree {
* public:
* int val;
* Tree *left;
* Tree *right;
* };
*/
Tree* findRightNode(Tree* tree, int target) {
if (!tree) return NULL;
queue<Tree*> Q;
Q.push(tree);
while (!Q.empty()) {
auto sz = Q.size();
for (int i = 0; i < sz; ++ i) {
auto p = Q.front();
Q.pop();
if (p->val == target) {
return i == sz - 1 ? NULL : Q.front();
}
if (p->left) Q.push(p->left);
if (p->right) Q.push(p->right);
}
}
return NULL;
}The Python implementation based on the double-ended queue to implement a Breadth First Search Algorithm:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | # class Tree: # def __init__(self, val, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def solve(self, tree, target): if tree is None: return None q = deque() q.append(tree) while len(q) > 0: sz = len(q) for i in range(sz): p = q.popleft() if p.val == target: if i == sz - 1: return None return q.popleft() if p.left: q.append(p.left) if p.right: q.append(p.right) return None |
# class Tree:
# def __init__(self, val, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def solve(self, tree, target):
if tree is None:
return None
q = deque()
q.append(tree)
while len(q) > 0:
sz = len(q)
for i in range(sz):
p = q.popleft()
if p.val == target:
if i == sz - 1:
return None
return q.popleft()
if p.left:
q.append(p.left)
if p.right:
q.append(p.right)
return None –EOF (The Ultimate Computing & Technology Blog) —
Last Post: Teaching Kids Programming - Binary Search Algorithm to Find First Bad Version
Next Post: Teaching Kids Programming - Sorting a Linked List using Merge Sort (Divide and Conquer)