An Interview Question: O(n) Algorithm to Find Abs(Max Left – Max Right)

Given an array of numbers (for simplicity, we use integers), find the maximum value of abs(max left – max right) where we separate the array into two. Mathematically, given a[0] to a[n – 1] where n is the lenght of the array, we want to find out the following:

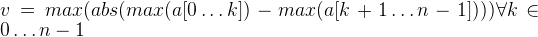
O(n) space and O(n) time

We can use two arrays e.g. maxleft and maxright to record the current maximum value from the left or right respectively. The third iteration goes from left to right to look for the maximum value of the difference.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

int proof(int nums[], int n) {
    vector <int> maxleft(n);
    maxleft[0] = nums[0];
    for (int i = 1; i < n; ++ i) {
        maxleft[i] = max(maxleft[i - 1], nums[i]);
    }
    vector<int> maxright(n);
    maxright[n - 1] = nums[n - 1];
    for (int i = n - 2; i >= 0; -- i) {
        maxright[i] = max(maxright[i + 1], nums[i]);
    }
    int ans = abs(maxleft[0] - maxright[0]);
    for (int i = 1; i < n; ++ i) {
        ans = max(ans, abs(maxleft[i] - maxright[i]));
    }
    return ans;
}

int proof(int nums[], int n) {
    vector <int> maxleft(n);
    maxleft[0] = nums[0];
    for (int i = 1; i < n; ++ i) {
        maxleft[i] = max(maxleft[i - 1], nums[i]);
    }
    vector<int> maxright(n);
    maxright[n - 1] = nums[n - 1];
    for (int i = n - 2; i >= 0; -- i) {
        maxright[i] = max(maxright[i + 1], nums[i]);
    }
    int ans = abs(maxleft[0] - maxright[0]);
    for (int i = 1; i < n; ++ i) {
        ans = max(ans, abs(maxleft[i] - maxright[i]));
    }
    return ans;
}

This C++ implementation is straightforward and we can also merge the second and the third iteration, which eventually makes O(2n) time and O(n) space. But could we do any better?

O(n) time and O(1) space

We can easily prove that maxleft and maxright is contionously incrementing and decrementing respectively. Also, we know that:

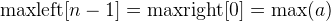
So, the overall answer must be the max(a) minus the 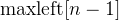or 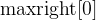. This gives the O(n) time and O(1) space complexity.

1
2
3
4
5
6
7

int findme(int nums[], int n) {
    int ans = nums[0];
    for (int i = 1; i < n; ++ i) {
        ans = max(ans, nums[i]);
    }
    return max(ans - nums[0], ans - nums[n - 1]);
}

int findme(int nums[], int n) {
    int ans = nums[0];
    for (int i = 1; i < n; ++ i) {
        ans = max(ans, nums[i]);
    }
    return max(ans - nums[0], ans - nums[n - 1]);
}

For example:

1
2
3

int nums[] = {2, 3, 6, 9, 11, 99, 88, 66, 1991, 3, 5, 22, 1, 2, 34, 6, 4, 5, 324, 5, 99};
cout << proof(nums, sizeof(nums) / sizeof(int)) << endl; // prints 1989
cout << findme(nums, sizeof(nums) / sizeof(int)) << endl; // prints 1989

int nums[] = {2, 3, 6, 9, 11, 99, 88, 66, 1991, 3, 5, 22, 1, 2, 34, 6, 4, 5, 324, 5, 99};
cout << proof(nums, sizeof(nums) / sizeof(int)) << endl; // prints 1989
cout << findme(nums, sizeof(nums) / sizeof(int)) << endl; // prints 1989

PS: We don’t want any sorting involved, because it at least is of complexity O(nlogn) for any sorting techniques.

–EOF (The Ultimate Computing & Technology Blog) —