The problem is from codeforces: http://www.codeforces.com/problemset/problem/192/A
The given input to this problem can be held by a four-byte integer (32-bit). It is to search for two numbers and such that .
The straightforward solution in Python is given below, which however will exceed the time limit: 2 seconds.
from math import sqrt
n = int(raw_input()) * 2
k = int(round(sqrt(n)))
found = False
for i in range(1, k):
if found:
break
for j in range(1, i):
if i * i + j * j + i + j == n:
print "YES"
found = True
break
if not found:
print "NO"
The above algorithm has the complexity of . However, there is a better algorithm, which runs in complexity of . The maximum input is therefore , which can be solved in bruteforce very quickly. This improved algorithm bruteforces the integers up to and computes the remainder. It checks if the remainder is the multiplication of .
from math import *
n = int(raw_input()) * 2
k = int(round(sqrt(n)))
found = False
for i in range(1, k):
r = n - i * i - i
x = int(floor(sqrt(r)))
if x * (x + 1) == r:
found = True
break
print "YES" if found else "NO"
–EOF (The Ultimate Computing & Technology Blog) —
GD Star Rating
loading...
550 wordsloading...
Last Post: Using Tkinter in Python GUI programming
Next Post: Bogo Sort Algorithm

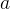 and
and 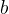 such that
such that 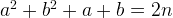 .
. 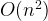 . However, there is a better algorithm, which runs in complexity of
. However, there is a better algorithm, which runs in complexity of 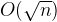 . The maximum input is
. The maximum input is 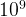 therefore
therefore 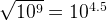 , which can be solved in bruteforce very quickly. This improved algorithm bruteforces the integers up to
, which can be solved in bruteforce very quickly. This improved algorithm bruteforces the integers up to 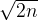 and computes the remainder. It checks if the remainder is the multiplication of
and computes the remainder. It checks if the remainder is the multiplication of 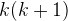 .
.